1. 연결리스트(Linked List)
- 추상형 자료형 중
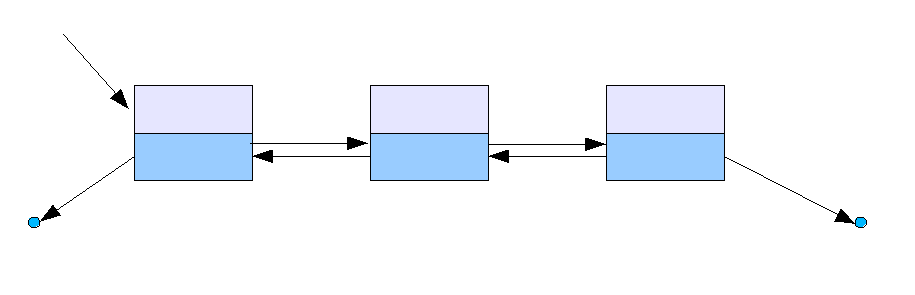
리스트(List)를 구체화 한 자료구조로, 데이터를 포함하는노드(Node)들이 다음(혹은 이전) 노드와 연결된 포인터를 통해 서로 연결되어 있는 형태이다. - 일반적으로
단순 연결 리스트(Singly Linekd List)와이중 연결 리스트(Doubly Linked List)로 나뉘며, 여기서는 이중 연결 리스트 형태로 구현하였다.- 이중 연결 리스트는 단순 연결 리스트와 달리 다음 노드와 함께 이전 노드를 가리키는 포인터도 존재한다.
- 이중 연결 리스트로 구현할 경우에는 노드 삭제 시에 삭제할 노드의 이전과 다음 노드를 서로 연결할 때 이전 노드에 접근하기 더욱 편리해진다.
- 일반적으로 연결 리스트에서 노드의 탐색 시 시간 복잡도가 O(N)이 되는데, 이전 노드를 참조하는 포인터가 존재하면 이를 찾는 데 O(1)로 줄어들기 때문이다.
2. 스위프트로 연결리스트 구현하기
2-1. 노드(Node) 구현
-
위에서 언급한 대로
노드(Node)는 데이터를 포함하고 있으며, 포인터를 통해 이전 노드와 다음 노드의 위치를 알 수 있다. -
리스트를 구성하는 노드(Node)가 될 클래스를 정의한다.
- 노드는 담고 있는 데이터를 프로퍼티로 가지고 있다.
- 노드에는 다양한 타입의 데이터가 들어가며, 이를 제네릭으로
<T>로 선언한다. - 노드 클래스의 프로퍼티는 데이터 뿐만 아니라 연결된 이전 노드(
prev)와 다음 노드(next)에 대한 참조도 프로퍼티로 가지게 된다.
class Node<T>{
var prev: Node<T>?
var next: Node<T>?
var data: T?
init(prev: Node<T>?, next: Node<T>?, data: T?){
self.prev = prev
self.next = next
self.data = data
}
}
2-2. Linked List
-
연결리스트 클래스 역시 제네릭
<T>를 선언하며, 여기서는 노드의 검색을 위해 해당 데이터가 비교 가능해야 하기 때문에Equatable을 같이 선언한다. -
연결 리스트 클래스는 리스트의 맨 처음과 끝에 해당하는 헤드 노드(
head) 와 테일 노드(tail) 을 각각 프로퍼티로 가지게 된다. -
연결 리스트 클래스는 각각 아래의 동작들에 대한 함수를 가지게 된다.
- 리스트가 비어있는 지 여부 판별
- 노드의 추가
- 노드의 탐색
- 노드의 삭제
-
위를 토대로 연결 리스트 클래스의 구조를 나타내면 아래와 같다.
class LinkedList<T: Equatable>{
//헤드노드
var head:Node<T>?
//테일노드
var tail:Node<T>?
//생성자
init(head: Node<T>?){
self.head = head
self.tail = head
}
//리스트 비어있는 지 판별
func isEmpty()->Bool
//맨 끝에 노드 추가
func append(node: Node<T>)
//입력받은 인덱스값에 해당하는 노드 검색
func search(index: Int)->Node<T>?
//입력받은 데이터를 가진 노드 검색
func search(data: T)->Node<T>
//리스트 사이즈 도출
func size()->Int
//원하는 인덱스에 노드 추가
func insert(node: Node<T>, index: Int)
//파라미터로 받는 데이터를 포함하는 노드 삭제
func remove(data: T)
}
리스트가 비어있는 지 검증하기
- 우선 노드가 비어있는 지의 판단은 단순히 헤드 노드가 nil인 지를 검증 하면 된다.
- 여기서 헤드 노드는 리스트의 시작이 되며, 리스트가 비어있다는 것은 노드의 시작 부분인 헤드 노드가 비어있다는 뜻이기 때문이다.
func isEmpty()->Bool{
return head==nil
}
리스트 맨 끝에 노드 추가하기
- 기본적으로 연결 리스트에서 노드의 추가는 리스트의 맨 끝 에서만 일어난다.(중간에 노드를 삽입하는 과정은 이후에 언급한다.)
- 리스트가 비어있다면 헤드 노드와 테일 노드를 추가할 노드로 두면 된다.
- 리스트가 비어있지 않다면 현재 테일 노드의 다음 노드로 추가할 노드를 두고, 추가한 노드를 테일 노드로 바꾸면 된다.
- 단, 테일 노드를 변경하기 전, 추가할 노드의
prev가 참조하는 노드를 기존 테일 노드로 둠에 주의한다.
- 단, 테일 노드를 변경하기 전, 추가할 노드의
func append(node: Node<T>){
if(isEmpty()){
head = node
tail = node
}else{
tail!.next = node
node.prev = tail
tail = node
}
}
노드 탐색하기
- 연결 리스트에서 특정 노드의 탐색은 노드의 시작부터 끝까지 순서대로 노드를 살펴보는 식으로 구현한다.
- 노드는 배열과 달리, 순차적으로 탐색해야 하기 때문에 시간복잡도가 O(N)이 된다.
- 구현할
search함수는 파라미터로 찾고자 하는 데이터 타입T를 받게 된다. - 리스트 클래스에서 제네릭으로 선언한
T는Equatable하기 때문에, 안에 들어있는 데이터의 참조가 서로 동일한 객체를 바라보는 지 비교하는 과정을 순차적으로 거치게 된다.
func search(data: T)->Node<T>{
var curr: Node<T> = self.head!
while curr.next != nil{
if(curr.data == data){
return curr
}
curr = curr.next!
}
return curr
}
- 파라미터로 찾고자 하는 데이터 외에,
Int타입의 인덱스값을 받아, 리스트의 해당 인덱스에 어떤 노드가 존재하는 지 탐색할 수도 있다.- 인덱스 0부터 파라미터로 받은 인덱스 직전까지 반복문을 돌면서, 헤드노드부터
curr이 참조하는 변수를 순서대로next로 바꿔가면 된다. - 반복문을 빠져나왔을 떄의
curr이 최종적으로 찾고자 하는 노드가 된다.
- 인덱스 0부터 파라미터로 받은 인덱스 직전까지 반복문을 돌면서, 헤드노드부터
func search(index: Int)->Node<T>?{
var curr:Node<T> = head!
if(index != -1){
for _ in 0..<index{
if curr.next == nil{
return nil
}else{
curr = curr.next!
}
}
}else{
return nil
}
return curr
}
원하는 위치에 노드 넣기
append와 달리insert는 파라미터로 넣고자 하는 노드와, 넣을 위치에 해당하는 인덱스값을 받게 된다.- 리스트가 비어있는 상태라면
append에서와 동일하게 헤드노드와 테일노드를 초기화하고 끝내면 된다. - 그렇지 않은 경우에는, 위에서 구현한 인덱스 기반
search를 통해, 새로운 노드를 넣을 위치의 이전에 존재하는 노드(prevTemp)를 찾고, 이를 기반으로 새로운 노드의 다음 노드가 될nextTemp를 찾으면 된다. - 찾고 나면 단순히 새로운 노드의
next를nextTemp로 바꾸고,prevTemp의next를 새로운 노드로 바꿔주면 된다. - 결과적으로 처음 파라미터로 받은 인덱스에 해당하는 노드와 파라미터로 받은 새로운 노드를 서로 바꿔주는 셈이 된다.
func insert(node: Node<T>, index: Int){
if(head == nil){
head = node
tail = node
return
}
guard let prevTemp = search(index: index-1) else{
node.next = head
head = node
return
}
guard let nextTemp = prevTemp.next else{
prevTemp.next = node
tail = node
return
}
node.next = nextTemp
prevTemp.next = node
}
노드 삭제하기
- 여기서는
remove의 파라미터로 노드가 포함하고 있는 데이터를 받았다. search함수를 통해 해당 데이터를 포함하는 노드를 찾은 후, 해당 노드의prev와next를 서로 이어주면 된다.- prev.next = next
- next.prev = prev
- 만일 데이터를 포함하는 노드가 헤드 노드이거나 테일 노드인 경우에는 별도로 처리해야 한다.
- 헤드 노드인 경우라면, 헤드 노드를 헤드 노드의 다음 노드로 바꿔준 후, 바뀐 헤드 노드의
prev를 nil로 처리한다. - 테일 노드인 경우라면, 반대로 테일 노드를 테일 노드의 이전 노드로 바꿔준 후, 바뀐 테일 노드의
next를 nil로 처리한다.
- 헤드 노드인 경우라면, 헤드 노드를 헤드 노드의 다음 노드로 바꿔준 후, 바뀐 헤드 노드의
func remove(data: T){
let nodeToBeRemoved: Node<T> = search(data: data)
if(nodeToBeRemoved.data == head!.data){
self.head = head!.next
head!.prev = nil
return
}else if(nodeToBeRemoved.data == tail!.data){
self.tail = tail!.prev
tail!.next = nil
return
}
let prev: Node<T> = nodeToBeRemoved.prev!
let next: Node<T> = nodeToBeRemoved.next!
prev.next = next
next.prev = prev
nodeToBeRemoved.prev = nil
nodeToBeRemoved.next = nil
}
- 최종적으로 완성된 LinkedList 클래스는 아래와 같다.
class LinkedList<T: Equatable>{
//헤드노드
var head:Node<T>?
//테일노드
var tail:Node<T>?
//생성자
init(head: Node<T>?){
self.head = head
self.tail = head
}
//리스트 비어있는 지 판별
func isEmpty()->Bool{
return head==nil
}
//맨 끝에 노드 추가
func append(node: Node<T>){
if(isEmpty()){
head = node
tail = node
}else{
tail!.next = node
node.prev = tail
tail = node
}
}
//입력받은 인덱스값에 해당하는 노드 검색
func search(index: Int)->Node<T>?{
var curr:Node<T> = head!
if(index != -1){
for _ in 0..<index{
if curr.next == nil{
return nil
}else{
curr = curr.next!
}
}
}else{
return nil
}
return curr
}
//입력받은 데이터를 가진 노드 검색
func search(data: T)->Node<T>{
var curr: Node<T> = self.head!
while curr.next != nil{
if(curr.data == data){
return curr
}
curr = curr.next!
}
return curr
}
//리스트 사이즈 도출
func size()->Int{
if(isEmpty()){
return 0
}else{
var size:Int = 1
var curr: Node<T> = self.head!
while curr.next != nil{
size += 1
curr = curr.next!
}
return size
}
}
//원하는 인덱스에 노드 추가
func insert(node: Node<T>, index: Int){
if(head == nil){
head = node
tail = node
return
}
//index = -1 인 경우에는 노드를 헤드노드 위치에 넣는 것으로 간주
guard let prevTemp = search(index: index-1) else{
//새로 넣을 노드와 헤드노드의 위치를 바꿔줌
node.next = head
head = node
return
}
//nextTemp가 존재하지 않는 경우는 노드를 테일노드 위치에 넣는 것으로 간주
guard let nextTemp = prevTemp.next else{
//새로 넣을 노드와 테일노드의 위치를 바꿔줌
prevTemp.next = node
tail = node
return
}
node.next = nextTemp
prevTemp.next = node
}
//파라미터로 받는 데이터를 포함하는 노드 삭제
func remove(data: T){
let nodeToBeRemoved: Node<T> = search(data: data)
if(nodeToBeRemoved.data == head!.data){
self.head = head!.next
head!.prev = nil
return
}else if(nodeToBeRemoved.data == tail!.data){
self.tail = tail!.prev
tail!.next = nil
return
}
let prev: Node<T> = nodeToBeRemoved.prev!
let next: Node<T> = nodeToBeRemoved.next!
prev.next = next
next.prev = prev
nodeToBeRemoved.prev = nil
nodeToBeRemoved.next = nil
}
}
3. 시간복잡도 검증
일반적인 이중 연결 리스트 연산의 시간 복잡도와, 구현한 클래스의 함수의 시간 복잡도를 서로 비교해본다.
- 이중 연결 리스트에서 일반적으로 노드 탐색 시 시간 복잡도는 O(N) 이다.
- 배열과 비교했을 때 연결 리스트가 가지는 단점이 된다.
- 배열의 경우 각 원소마다 고유의 인덱스가 있기 때문에, 인덱스를 알면 바로 접근하므로 O(1)이 되기 때문이다.
- 연결 리스트의 경우에는 매번 헤드 노드에서 시작해서, 찾고자 하는 노드가 나타날 때 까지 순차적으로 탐색해야 하기 때문에 최악의 경우에는 리스트의 맨 끝까지 가야 하므로 O(N)이 되는 것이다.
- 위의 LinkedList의
search함수 두 개 모두 순차적으로 노드를 순회하는 아래의 반복문으로 인해, 실행 시 시간복잡도는 O(N)이 된다.
//0부터 인덱스까지 순차적으로 검색
for _ in 0..<index{
if curr.next == nil{
return nil
}else{
curr = curr.next!
}
}
//헤드노드에서 시작해서, 순차적으로 다음 노드를 탐색
var curr: Node<T> = self.head!
while curr.next != nil{
if(curr.data == data){
return curr
}
curr = curr.next!
}
- 탐색과 달리 이중 연결 리스트에서 노드의 추가 및 삭제 연산 시의 시간 복잡도는 O(1) 이 된다.
- 이는 배열과 달리 연결 리스트가 가지는 장점이 된다.
- 배열의 경우 배열 중간에 위치한 특정 원소를 추가 및 삭제 할 경우, 나머지 원소들의 위치를 모두 재조정해야 하기 때문에 최악의 경우 시간복잡도가 O(N)이 된다.
- 연결 리스트의 경우에는, 추가 및 삭제할 위치만 찾아서 추가할 노드와 이어질 노드들의 참조값만 바꿔주면 되기 때문에 O(1)이 된다.
- 위의 LinkedList의
append,remove모두 별도의 반복문 없이 노드들의 참조값만 바꾸고 있기 때문에 함수 실행 시의 시간복잡도가 O(1)이 된다.
//노드 추가 시 맨 끝의 참조값만 바꿔줌
tail!.next = node
node.prev = tail
tail = node
//노드 삭제 시 참조값만 바꿔줌
let prev: Node<T> = nodeToBeRemoved.prev!
let next: Node<T> = nodeToBeRemoved.next!
prev.next = next
next.prev = prev
nodeToBeRemoved.prev = nil
nodeToBeRemoved.next = nil